Cloth Simulation
PlatformWin32 LanguageC/C++ GraphicsOpenGL
Description
This project is a soft body physics system that simulates cloth. The cloth is comprised of particle masses constrained by a spring-damper mechanism. The simulation can create an arbitrarily sized cloth with a user-definable amount of rows and columns. The cloth can further be constrained by fixing any particle, so that it has no velocity or acceleration. The beginning orientation of the cloth can be selected as well. The forces acting on the cloth, in addition to the internal spring forces, are gravity, air resistance, wind, and friction due to collision with other objects. The fixed points can also be released during the simulation allowing the cloth to fall freely to the ground or fly through the air on the wind. I have implemented two types of collision response – impulse force and repulsion force.
The buttons control starting and stopping the simulation and releasing the fixed particles. There is also a scroll bar that can be used to control the intensity of the wind. To the right of the OpenGL window, which displays the graphical simulation, is a long list of labels that describe the current attributes for the simulation. Each of these attributes is a variable that affects the simulation and each can be altered to affect the outcome. The menus allow you to configure the cloth in various ways.
This application can be run on Win32 systems with OpenGL. The window library used in the program was created by Dr. John McDonald of DePaul University.
Construction
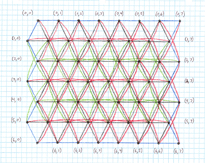
The cloth is constructed by using an offset grid, which creates an equilateral triangle mesh, as shown below. The first picture shows the alignment of the structural springs (pictured in black) with a particle mass at each vertex. The second picture shows the full structure of the cloth, including the shear and bend springs (pictured in red and green) in addition to the structural springs.
This layout allows the cloth to move more freely than a standard grid, but the down-side is the much greater complexity and difficulty of implementation. Each vertex has a maximum of 12 springs connecting it to its neighbors. This complexity also creates problems with trying to scale the cloth to larger sizes, as the increase in springs needed is exponential. The more refined the cloth is, the longer it takes to render each frame.
The spring force provides the structure and maintains the form of the cloth, whereas the damping prevents the springs from jumping around too much and also provides a measure of numerical stability. The right balance between spring force and damping is crucial to the realism of the cloth. Too much damping will cause the cloth to lose its soft body motion characteristics, too little and the cloth will blow apart at the seams.
In addition to the spring characteristics, the particle mass characteristics can also be adjusted. In my simulation, I created the cloth with equal mass at each particle. This has the effect of giving the edges a greater weighting in terms of their mass than the interior particles. Normally the mass is proportional to the number of surrounding particles. However, giving the edge particles some extra mass keeps the edges from becoming unruly and is tantamount to a tailor basting or weighting the edge of a garment with additional thread.
Integration
Once the cloth has been weaved, we apply forces to it and see how it responds. This involves calculating the total force applied to a particle, then calculating the resulting acceleration of each particle, and finally updating its velocity and position. Since the simulation requires taking incremental steps in time to determine the next move coupled with the fact that floating point arithmetic is not exact, numerical instability can result rather quickly without a proper integration scheme. I used a fourth order Runge-Kutta based algorithm to perform the integration. The algorithm successfully balances precision with computation time and achieves good numerical stability. Even with this precision however, the complexity of this simulation requires a very small time step on the order of 10-4.
Collision Detection and Response
I currently have no provision for calculating cloth to cloth collisions, and in fact, with a high enough velocity the cloth will actually pass through itself before righting itself once more.
The impulse force used for collision response provides the user with two additional variables that need to be tweaked – the coefficient of restitution, kr , and the coefficient of friction, kf. The coefficient of restitution, determines the level of elasticity of the collision between the two bodies, with 0 equaling a perfectly inelastic collision and 1 being a perfectly elastic collision. The coefficient of friction affects the tangential velocity of the collision and affects the measure of energy converted to sliding friction between the two objects. In my simulation, I typically use a near total inelastic collision for cloth. The friction coefficient can be altered depending on the desired effect. A lower friction results in the cloth sliding well over surfaces and the reverse is true for high friction. Both situations may be desirable at times.